[Code]
The closed Boolean semiring,
[User's Manual]
[Code]
The closed Boolean semiring, ![]() , suffices for processing simple
partial orders of types with no features, often called type
hierarchies. For type signatures with feature appropriateness
conditions and value restrictions on those features, this is not
enough however.
, suffices for processing simple
partial orders of types with no features, often called type
hierarchies. For type signatures with feature appropriateness
conditions and value restrictions on those features, this is not
enough however.
We can think of 0 and 1 in ![]() as constituting a very small type
hierarchy, as shown in Figure 3.8. If
as constituting a very small type
hierarchy, as shown in Figure 3.8. If
![]() corresponds to 1, and
corresponds to 1, and ![]() to 0, then unification in this
hierarchy corresponds to Boolean OR. We can also write this as in
Figure 3.9, in which the trivial type
hierarchy, consisting of just
to 0, then unification in this
hierarchy corresponds to Boolean OR. We can also write this as in
Figure 3.9, in which the trivial type
hierarchy, consisting of just ![]() , has been bottom-lifted to
add a new bottom,
, has been bottom-lifted to
add a new bottom,
![]() . Because bottom-lifting preserves
meet-semi-latticehood, we can trivially extend unification,
. Because bottom-lifting preserves
meet-semi-latticehood, we can trivially extend unification, ![]() ,
to any
,
to any
![]() where
where ![]() is a finite meet semi-lattice. Now,
we need something to correspond to AND:
is a finite meet semi-lattice. Now,
we need something to correspond to AND:
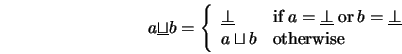
|
|
Notice that we can define this for all ![]() , not just the trivial type
hierarchy, because in all type hierarchies,
, not just the trivial type
hierarchy, because in all type hierarchies, ![]() and therefore its
extension to
and therefore its
extension to
![]() and to
and to
![]() , are total functions,
and there is a least element. As can easily be verified:
, are total functions,
and there is a least element. As can easily be verified:
The existence of a greatest element ensures that ![]() and
and
![]() are closed in
are closed in
![]() . Without loss of generality,
we can assume that the greatest element,
. Without loss of generality,
we can assume that the greatest element, ![]() , does not explicitly
appear in
, does not explicitly
appear in ![]() , and that it does not occur anywhere else in the
signature, e.g., in appropriateness conditions.
, and that it does not occur anywhere else in the
signature, e.g., in appropriateness conditions. ![]() can be smashed
onto any such
can be smashed
onto any such ![]() , and is typically implemented as type unification
failure in the original signature. Figure 3.10 shows
the type hierarchy in Figure 3.1
, and is typically implemented as type unification
failure in the original signature. Figure 3.10 shows
the type hierarchy in Figure 3.1
![]() -lifted and
-lifted and ![]() -smashed to form its induced closed semiring.
-smashed to form its induced closed semiring.
The benefit of using ![]() is that it allows us to generalize to
other computations on signatures that require matrices with types in
them rather than just 0s and 1s. The subsumption matrix of
is that it allows us to generalize to
other computations on signatures that require matrices with types in
them rather than just 0s and 1s. The subsumption matrix of ![]() can
still be constructed using
can
still be constructed using
![]() and
and ![]() in place of 0 and 1,
respectively.
in place of 0 and 1,
respectively.
[Code]
In the logic of typed feature structures, appropriateness conditions
take the form of a restriction on which types can bear a particular
feature, and which types that feature's value can have.
Feature Introduction eliminates a source of disjunction in inferring types from feature names in descriptions. By having a unique introducing type, it is possible to apply appropriateness in the other direction immediately to infer some of the other features that must also exist, along with the types of their values.
In practice, signature declarations specify appropriateness only by declaring (1) where a feature is introduced, along with the type its value must have and (2) where a feature takes on a value whose type cannot be inferred to be the least type that satisfies Upward Closure and/or Right Monotonicity given its value on supertypes. The type to which a feature's value is constrained is called a value restriction. Figure 3.11, for example, is Figure 3.1 with appropriateness declarations added.
F is appropriate to a, for example, with value restriction,
In order to enforce this view of appropriateness conditions on ![]() , we
can build a matrix over
, we
can build a matrix over ![]() for these declarations:
for these declarations:
The uniqueness of ![]() , when it exists, is guaranteed by the fact that
, when it exists, is guaranteed by the fact that
![]() is a partial function. The value declaration matrix for
Figure 3.11 is shown in
Figure 3.12. The entry for type
is a partial function. The value declaration matrix for
Figure 3.11 is shown in
Figure 3.12. The entry for type ![]() , feature H is
, feature H is
![]() because H is declared as appropriate to
because H is declared as appropriate to ![]() with its value
restricted to
with its value
restricted to ![]() .
.
Notice that
![]() is being used here as a place-holder for pairs
of type, t and feature, F, for which F is not
appropriate to t. We use
is being used here as a place-holder for pairs
of type, t and feature, F, for which F is not
appropriate to t. We use
![]() rather than
rather than ![]() so that
feature introduction (with a value restriction of
so that
feature introduction (with a value restriction of ![]() or greater)
still respects Right Monotonicity.
or greater)
still respects Right Monotonicity.
Premultiplying ![]() by the transpose of
by the transpose of ![]() closes the appropriateness
declarations under subsumption.
closes the appropriateness
declarations under subsumption. ![]() is thus something other
than
is thus something other
than
![]() iff feature
iff feature ![]() is appropriate to type
is appropriate to type ![]() . The value
restriction matrix of Figure 3.11 is shown in
Figure 3.13. Notice that the entry for type e,
feature H is also b because e inherits H from
d.
. The value
restriction matrix of Figure 3.11 is shown in
Figure 3.13. Notice that the entry for type e,
feature H is also b because e inherits H from
d.
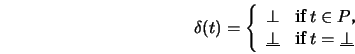
Along the way, we can also compute those introducing types:
[Code]
Because of Right Monotonicity, join-reducible types can not only
multiply inherit features, but also inherit value restrictions on the
same feature from two or more different branches; and these must be
consistent. Figure 3.15 shows an example of this.
The value declaration matrix for Figure 3.15 is given in Figure 3.16.
The value restriction matrix of Figure 3.15 is given in Figure 3.17. Without h, the entry for d would have been
All types must have a finite most general satisfier, a finite least
informative feature structure of that type that respects
appropriateness conditions. This means that appropriateness
conditions may not conspire so as to require a feature structure of
type t to have a proper substructure of type either t or a
subtype of t. Very often, the appropriateness conditions will
allow a subtype of t to occur, but that is not the same
thing. Non-empty lists, for example, have a tail appropriate to
lists, of which non-empty lists are a subtype. That makes lists a
recursive data type, but lists still have finite most general
satisfiers. The former kind of appropriateness cycle can very
naturally be described using ![]() .
.
In practice, this transitive closure can be computed directly from
![]() , without explicitly constructing
, without explicitly constructing ![]() .
.
Not all type signatures are statically typable. This means that there are some signatures for which the result of unifying two feature structures that obey appropriateness must be reverified as obeying appropriateness. Although these signatures are technically valid ones, systems that process with LTFS normally check for static typability because of the computational cost of this run-time verification. Signatures that are not statically typable are those that do not satisfy the following condition:
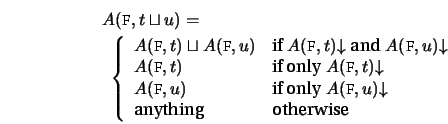
Viewed in terms of ![]() , join preservation is a linear dependence
condition among consistent types--recall that in
, join preservation is a linear dependence
condition among consistent types--recall that in ![]() ,
, ![]() corresponds to the additive operator. In a join-preserving signature,
joins cannot add new information to the system, apart from introducing
new features.
corresponds to the additive operator. In a join-preserving signature,
joins cannot add new information to the system, apart from introducing
new features.