- ... Tübingen2.1
- ©2003, Detmar Meurers, Thilo Götz and Dale Gerdemann.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... editor.2.2
- Also, be aware when mixing tabs and spaces: If
you type in a space and then a tab, the space may become invisible
on the screen, but still counts when calculating the indentation
level!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... consistently.2.3
- We feel that the advantage of this approach
is that it allows the hierarchical nature of the type hierarchy to
be seen without too much obscuring syntax. A purely graphical type
hierarchy interface would be even better, but this is as close as
we could come to a graphical presentation within the confines of
ASCII. It must also be admitted that using level of indentation
to indicate subtypes a certain level of complexity. It is no
longer possible to give a BNF definition of the type hierarchy
since the level-of-indentation must be passed around as a context
sensitive feature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (
&).2.4
- The ampersand is not necessary but it is
recommended. Our experience has shown that unintended multiple
inheritance, by accidently using the same type name for different
purposes, is a common error. If the ampersand is omitted, the
system will give a non-fatal error message.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
matrices,3.1
- Note that the corresponding Boolean algebra for
these matrices is a semiring where
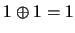 because as
mentioned above, in a Boolean semiring, the additive operator
because as
mentioned above, in a Boolean semiring, the additive operator
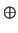 corresponds to OR.
corresponds to OR.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,3.2
-
 means defined.
means defined.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... University8.1
- ©2003, Vanessa Metcalf, Detmar Meurers and Markus Dickinson
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... each.8.2
- We actually translate a
copy of each description into a feature structure, since desc2fs/3
adds type information to Prolog variables, thereby making them
unrecognizable as such to var/1. We rely on Prolog variables in the
descriptions to signal the presence of a path equality in the
lexical rule descriptions. We keep track of this information in
order to avoid creating undesirable path equalities in the frames.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... succeeded.8.3
- To obtain the correct
follows relation for a lexical rule, however, information from the
input specification should to be transferred to the output, ideally
via a generalized frame predicate. Currently, we include a lexical
rule on the follows list if unification succeeds utilizing at least
one of the clauses defining the frame predicate for the lexical rule
in question.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... chart:9.1
- Note that
for ease of exposition, we are showing a simplified version of the
code here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... below:10.1
- VF stands for Vorfeld, CF for
Complementiser Field (left sentence-bracket), MF for Mittelfeld, VC
for Verbal Complex (right sentence-bracket), and NF for Nachfeld
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Prolog.12.1
- The above information has been adapted from
http://wombat.doc.ic.ac.uk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.