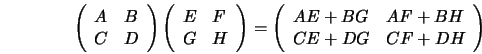To transitively close a matrix in its ZCQ-representation, we first recurse on its diagonal quadrants, as suggested by (*), to obtain
[Code--Upper Triangular Transitive Closure]
To transitively close a matrix in its ZCQ-representation, we first
recurse on its diagonal quadrants, as suggested by (*), to obtain
![]() and
and ![]() . We then compute
. We then compute ![]() with two matrix
multiplications. Matrix multiplication in ZCQ is given by the
quadrant-based recursive formulation:
with two matrix
multiplications. Matrix multiplication in ZCQ is given by the
quadrant-based recursive formulation: