


Next: Transitive Closure with ZCQ
Up: Signature Compilation
Previous: Zero-Counting by Quadrants
Contents
[Code--ZCQ Matrix]
In Prolog, we represent the Zero-Counting-Quadrant (ZCQ) Matrices
discussed above using the data structure presented in this section.
-
- zcm(A,B,D,C) is the basic data structure.
Each argument in zcm/4 stands for a quadrant in the matrix.
The correspondence is shown in Figure 3.4. This is a
recursive structure which means that each one of A, B,
C, or D is itself a zcm/4 or any of the other data
structures presented below.
Figure 3.4:
Matrix quadrants corresponding to arguments in
zcm(A,B,D,C)
- The number 0 stands for a sparse matrix of 0s.
- zcu(A,B,C) represents an upper-triangular
matrix as shown in Figure 3.5. Because it is an
upper-triangular matrix, we already know that D is 0. The
values of A and C need only be either zcu/3
themselves or 1. The value of B can be zcm/4 or any of
the base cases mentioned below.
Figure 3.5:
An upper triangular matrix corresponding to
zcu(A,B,C)
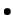
- Base Cases:
- The number 1 stands for a
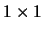 matrix of 1.
matrix of 1.
- zc12(A,B) is a
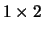 matrix shown in
Figure 3.6
matrix shown in
Figure 3.6
Figure 3.6:
A 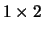 matrix corresponding to zc12(A,B)
matrix corresponding to zc12(A,B)
- zc21(A,D) stands for a
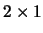 matrix shown in
Figure 3.7
matrix shown in
Figure 3.7
Figure 3.7:
A 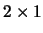 matrix corresponding to zc21(A,D)
matrix corresponding to zc21(A,D)



Next: Transitive Closure with ZCQ
Up: Signature Compilation
Previous: Zero-Counting by Quadrants
Contents
TRALE Reference Manual