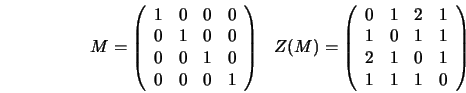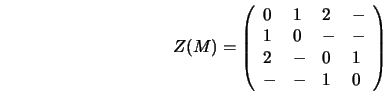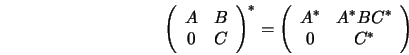
The algorithm used in ALE is a specialized sparse matrix
multiplication algorithm for semirings. Sorting of the rows and
columns of the matrix takes place through the standard depth-first
topological sorting algorithm provided in the last section. In such
matrices,3.1 the transitive closure of the matrix
can be calculated as:
[Code--Upper Triangular Transitive Closure]
Two functions are used to recursively divide a matrix evenly into
quadrants. For any ![]() and
and ![]() such that
such that ![]() , let
, let ![]() be defined such that:
be defined such that:
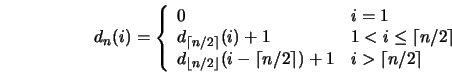
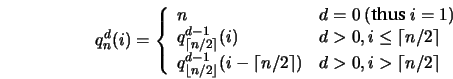
Given a matrix ![]() , we shall say that a submatrix is rooted
at
, we shall say that a submatrix is rooted
at ![]() iff
iff ![]() is its leftmost, uppermost coordinate in
is its leftmost, uppermost coordinate in ![]() .
.
Given ![]() ,
, ![]() ,
, ![]() and
and ![]() such that
such that
![]() , and
, and
![]() , let
, let
![]() .
When we divide an
.
When we divide an ![]() matrix
matrix ![]() evenly into quadrants, then
the largest quadrant rooted at
evenly into quadrants, then
the largest quadrant rooted at ![]() will be
will be
![]() in size. It can be proven that if
in size. It can be proven that if ![]() and
and
![]() differ by no more than 1 in the original matrix, then these two
dimensions will differ by no more than 1.
differ by no more than 1 in the original matrix, then these two
dimensions will differ by no more than 1.
Now, given a Boolean matrix ![]() , there is a unique matrix
, there is a unique matrix ![]() over
the non-negative integers such that the value of
over
the non-negative integers such that the value of ![]() is the
size of the largest zero-quadrant rooted at
is the
size of the largest zero-quadrant rooted at ![]() in the largest
quadrant rooted at
in the largest
quadrant rooted at ![]() . If this largest zero-quadrant is not
square, then we use the larger of its dimensions as the value. As a
simple example, consider the
. If this largest zero-quadrant is not
square, then we use the larger of its dimensions as the value. As a
simple example, consider the ![]() identity matrix as
identity matrix as ![]() :
: