


Next: Zero-Counting by Quadrants
Up: Signature Compilation
Previous: Monoids, Rings, Quasi-Rings, and
Contents
Topological Sorting
[Code--Topological Sorting]
Before creating a subsumption matrix for a type hierarchy, ALE
needs to topologically sort the types. The topological sorting of the
types in a type hierarchy ensures the placement of more general types
before more specific ones. This is performed through a depth-first
traversal of the hierarchy. For example, to topologically sort the
type hierarchy presented in Figure 3.1, we
start at 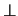 . Once we have added
. Once we have added 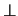 to our list of
topologically sorted types, we continue to a, then b.
Since b does not have any subtypes, we go back to a and
move to c. Carrying on in the same fashion and adding new types
to the list will result in [
to our list of
topologically sorted types, we continue to a, then b.
Since b does not have any subtypes, we go back to a and
move to c. Carrying on in the same fashion and adding new types
to the list will result in [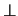 , a, b, c, e, d]. Building a subsumption matrix based on this sorting
results in an upper-triangular sparse matrix meaning that the
lower left quadrant of the matrix consists only of zeros as in figures
3.2 and 3.3.
, a, b, c, e, d]. Building a subsumption matrix based on this sorting
results in an upper-triangular sparse matrix meaning that the
lower left quadrant of the matrix consists only of zeros as in figures
3.2 and 3.3.
TRALE Reference Manual