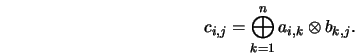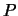 is a set closed under
is a set closed under  :
: 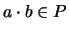 , for all
, for all
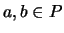 ,
,
 is an associative binary operator:
is an associative binary operator:
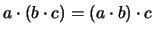 , for all
, for all 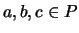 , and
, and
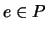 is an identity for
is an identity for  :
:
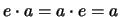 for
all
for
all 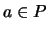 .
.
If ![]() is a quasi-ring, then multiplication of matrices is
well-defined and has certain nice properties such as associativity and
the existence of an identity.
is a quasi-ring, then multiplication of matrices is
well-defined and has certain nice properties such as associativity and
the existence of an identity.