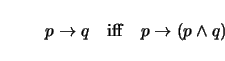
TRALE theories can use all of the declarations available to ALE . These include relations, lexical entries, lexical rules, extended phrase structure rules, and Prolog-like definite clauses over typed feature structures. They also include one extra, complex-antecedent constraints, which is discussed in the following section.
ALE's constraints are more restricted in the sense that the antecedent (left-hand side) of a constraint can only be a type. ALE constraints have the following forms:
or
where the antecedent, t, is a type and the consequent (right-hand side), Desc, is the description of the constraint. These constraints apply their consequents to all feature structures of type t, which is to say that they are universally quantified over all feature structures and are triggered based on subsumption, i.e., Desc and Goal are not necessarily applied to feature structures consistent with t, but rather to those that are subsumed by the most general satisfier of t, as given by a constraint-free signature. For example, the constraint:
a cons (f:X,g:=\=X)
states that the values of the F and G features of any object of type a or a type subsumed by a must not be structure-shared. If a goal is specified in a constraint, the constraint is satisfied only if the goal succeeds.
TRALE generalizes this to allow for antecedents with arbitrary function-free, inequation-free antecedents. TRALE constraints are defined using the infix operator, *>/2, e.g.:
This constraint executes foo/1 on feature structures with F value minus and G value plus. These are also universally quantified, and they are also triggered based on subsumption by the antecedent, not unification. For example, in the above constraint, if a feature structure does not have an F value, minus, and a G value, plus, yet, but is not inconsistent with having them, then TRALE will suspend consideration of the constraint until such a time as it acquires the values or becomes inconsistent with having them. These constraints are thus consistent with a classical view of implication in that the inferences they witness are sound with respect to classical implication, but they are not complete. On the other hand, they operate passively in the sense that the situation can arise in which several constraints may each be waiting for the other for their consequents to apply. This is called deadlock. An alternative to this approach would be to use unification to decide when to apply consequents, or some built-in search mechanism that would avoid deadlock but risk non-termination. Of the two, deadlock is preferable. Additional (constraint) logic programs can be written to search the space of possible solutions in a way suited to the individual case if there are deadlocked or suspended constraints in a solution.
Variables in *> constraints are implicitly existentially quantified within the antecedent. Thus:
applies the consequent when F's and G's values are structure-shared. In other words, it applies the consequent if there exists an X such that F's and G's values are both X. In addition, the consequent of the above-mentioned constraint implicitly applies only to feature structures for which F and G are both appropriate. Path equations can be used in antecedents to explicitly request structure-sharing as well. The following constraint is equivalent to the one above:
A singleton variable in the antecedent results in no delaying itself apart from the implicit appropriateness conditions. Variables occurring in the consequent are in fact bound with scope that extends over the consequent and relational attachments. Thus, in the following example:
the first argument passed to foo/2 is the very X that is the value of both F and G. This use of variables on both sides of the implication is a loose interpretation consistent with common practice in linguistics. With a classical interpretation of implication, it is always true that:
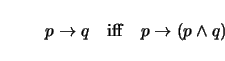
Thus:
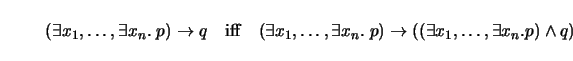
Note that, according to the classical interpretation,
![]() is not in the scope of the existential quantifiers. TRALE ,
however, bends this rule taking the latter to be equivalent to:
is not in the scope of the existential quantifiers. TRALE ,
however, bends this rule taking the latter to be equivalent to:
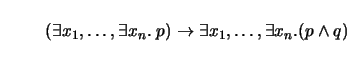
Here, ![]() is in the scope of the
is in the scope of the
![]() . Consequently, if the genuine equivalence is desired,
one must ensure that
. Consequently, if the genuine equivalence is desired,
one must ensure that
![]() do not occur in
do not occur in ![]() , in
which case
, in
which case
![]() and
and
![]() are equivalent.
Requiring this extra variable hygiene is the price of permitting
this non-equivalent use of implication and quantification as the
default, rather than what is logically valid. An example of such a
relaxed use of such rules in linguistics is provided below:
are equivalent.
Requiring this extra variable hygiene is the price of permitting
this non-equivalent use of implication and quantification as the
default, rather than what is logically valid. An example of such a
relaxed use of such rules in linguistics is provided below:
spec_dtr:(head:noun,
index:Ind)
*> head_dtr:(head:verb,
index:Ind).
The above constraint is formulated so as to assure subject-verb agreement by enforcing structure-sharing between the INDEX feature of the subject and that of the verb. In the strict interpretation, the second instance of the variable Ind would have broad scope (existentially quantified over the entire clause), and thus be possibly different from the Ind in the antecedent. TRALE's interpretation of this, however, assumes they are the same. As mentioned above, if the strict interpretation is desired, a different variable name must be used in the consequent of this constraint.
In some languages, the form of the verb depends on the type of eventuality denoted by the sentence. In Czech, for example, it is generally the case that if an event is total (i.e. completed as opposed to simply terminated), the verb that denotes that event surfaces in the perfective form. This rule can be enforced as the following constraint in the grammar. Note that since the constraint applies to a type rather than a particular description, we could use an ALE constraint (cons/2), too.
(sentence,event:total) *>
synsem:(local:(cat:(head:(vform:perf)))).
This constraint applies its consequent to all feature structures of type sentence with the required EVENT value.
Another example of a complex-antecedent constraint can be found in HPSG's Binding Theory, which refers to the notions of o-binding and o-commanding. O-binding is defined as follows (see Pollard and Sag, 1994, p. 253-54):
``Y (locally) o-binds Z just in case Y and Z are coindexed and Y (locally) o-commands Z. If Z is not (locally) o-bound, then it is said to be (locally) o-free.''
Pollard and Sag define o-commanding as follows:
``Let Y and Z be synsem objects with distinct LOCAL values, Y referential. Then Y locally o-commands Z just in case Y is less oblique than Z...
``Let Y and Z be synsem objects with distinct LOCAL values, Y referential. Then Y o-commands Z just in case Y locally o-commands X dominating Z.''
Based on these notions, HPSG's Binding Theory is phrased as the following three principles (ibid):
HPSG Binding Theory:
Principle A. A locally o-commanded anaphor must be locallyo-bound.
Principle B. A personal pronoun must be locally o-free.
Principle C. A nonpronoun must be o-free.
A simplified version of Principle A can be written as a constraint over all head-comple-ment structures (head_comp_struc) as follows:
% BINDING THEORY
% PRINCIPLE A
head_comp_struc *> (spec_dtr:(synsem:content:
(X,
index:IndX)),
comp_dtr:(synsem:content:
(Y,ana,
index:IndY)))
goal (local_o_command(X,Y) ->
IndX = IndY; true).
(X = X) if true.
The above ALE constraint makes sure that for all head_comp_struc type objects, if the complement daughter is anaphoric and locally o-commanded by the specifier, then the two daughters must be coindexed. The definition ``(X = X) if true'' is provided because ALE does not come with a built-in equality relation defined over descriptions. We leave the definitions of local_o_command/2 and o_command/2 to the reader.
An alternative is to formulate the constraint in the following manner:
% BINDING THEORY % PRINCIPLE A (Alternate formulation): (spec_dtr:(synsem:content:(X,index:IndX)), comp_dtr:(synsem:content:(Y,ana,index:IndY))) *> bot goal (local_o_command(X,Y) -> IndX = IndY; true). (X = X) if true.
The above constraint applies to any description subsumed by the antecedent. If the first daughter's index locally o-commands the second's, then they should be coindexed. Bot results in no additional description be added. Alternatively, one could use an anonymous variable, ``_''.
Let us now see how Principle B can be written as a TRALE complex-antecedent constraint:
% Binding Theory % PRINCIPLE B: (spec_dtr:(synsem:content:(X,index:Ind)), comp_dtr:(synsem:content:(Y,ppro,index:Ind))) *> bot goal (local_o_command(X,Y) -> fail; true).
This constraint states that for all descriptions with specifier and complement daughters, if the latter is a personal pronoun and locally o-commanded by the former, then the two daughters must not be coindexed.
Analogously, Principle C can be encoded as follows:
% BINDING THEORY % PRINCIPLE C: (spec_dtr:(synsem:content:(X,index:Ind)), comp_dtr:(synsem:content:(Y,npro,index:Ind))) *> bot goal (o_command(X,Y) -> fail; true).
This last constraint states that for all descriptions with specifier and complement daughters, if the second one is a nonpronoun (npro), then it must not be o-commanded by the first and coindexed with it.